
La combinatoria es mucho más divertida de lo que parece.
¿Qué es la combinatoria?
Son técnicas de recuento que están al alcance de cualquiera. La combinatoria es el arte de contar números. Algunas veces, durante una conversación surgen preguntas de este tipo:
- ¿Cuántas matrículas de coches son posibles en España?
- ¿Cuál es el número de quinielas de fútbol que hay que hacer para acertar 14 con seguridad?

Pronto lo sabrás. Si quieres, claro.
En este artículo trataré de ofrecerte un esquema de combinatoria para que te quede todo más claro.
Tal vez hayas intentado resolver las primeras preguntas y no te acuerdes de cómo proceder. Es normal, lo que no se practica se olvida.
La combinatoria es una rama de las matemáticas con mucho potencial. En menos de un minuto es capaz de solucionar preguntas aparentemente complejas. Básicamente analiza las diversas formas de realizar agrupaciones con los elementos de un conjunto, formándolas y calculando su número.
Los problemas de combinatoria siempre han llamado la atención de los matemáticos. Uno de los más célebres es el problema de los cuadrados mágicos. Igualmente es muy famoso el triángulo de Pascal, que además de tener unas propiedades impresionantes, la disposición de sus números coincide exactamente con los números combinatorios.
Pero fue el genial Leonhard Euler quien desarrolló a principios del siglo XVIII una auténtica escuela de matemática combinatoria.
Mi humilde intención es hacer un breve resumen de las técnicas de recuento y de conceptos sencillos, para que entindas bien todo el esquema de combinatoria, a través de algunos ejemplos sencillos.
Zarpamos!
Esquema de combinatoria. Técnicas de recuento
1. Principio de multiplicación
Se utiliza cuando tenemos n1 opciones de escoger un objeto, n2 opciones de escoger un segundo objeto, n3 opciones de escoger un tercer objeto etc. Matemáticamente podemos representarlo así: n1·n2·n3· …nn
Una marca de coches comercializa un modelo en tres versiones (3 puertas, 5 puertas y familiar). El motor puede ser de dos tipos (diésel o gasolina). Hay cuatro colores disponibles. ¿Cuántos tipos de coches diferentes se fabrican para este modelo?
Aplicando el principio de multiplicación tenemos que 3·2·4 = 24 coches diferentes
Fácil, ¿verdad?
Ahora ya estás en condiciones de responder a la primera pregunta del artículo. ¿Cuántas matrículas? Te doy una pista. En cada cifra hay 10 opciones y en cada letra 19 (no se cuentan las vocales, ni la ñ, ni la q). Tenemos para muchos años ...
Me gustaría mucho saber cuantas posibilidades de matrículas de coche hay en tu país.
2.Variaciones ordinarias o sin repetición
En una carrera de atletismo participan ocho corredores. ¿De cuántas maneras se pueden asignar las tres medallas?
La medalla de oro la pueden obtener los ocho corredores (aunque haya favoritos), con la de plata nos quedan 7 posibilidades, y con el tercer puesto sólo 6.
Es decir, tenemos variaciones ordinarias de 8 elementos tomados de 3 en 3.
En general, llamamos variaciones ordinarias de m elementos tomados de n en n (n≤m), a los distintos grupos que se pueden formar con m elementos de tal forma que:
- En cada grupo entran n elementos diferentes
- Influye el orden de colocación
Generalizando, tenemos:
Ehhh, que aparece un signo de admiración y unos corchetes. Me pierdooo. Tranquilo, te explico un par de cosillas, para que puedas comprobar que la fórmula general se cumple siempre.
El factorial de un número (n!) es el producto de lo n primeros números naturales. Por ejemplo 5! = 5·4·3·2·1
Esto es un número combinatorio:
3.Variaciones con repetición
¿Cuántos números de tres cifras se puede formar con los dígitos: 1, 2, 3, 4, 5 ?
En este caso tenemos que m = 5 y n = 3
No entran todos los elementos. De 5 dígitos entran sólo 3.
Sí importa el orden. Son números distintos el 123, 231, 321.
Sí se repiten los elementos.
En general, llamamos variaciones con repetición de m elementos tomados de n en n, a los distintos grupos que se pueden formar con m elementos de manera que:
En el caso que nos ocupa,tenemos que VR5,3 = 5·5·5= 125 Fíjate que tenemos 3 factores
Con las 10 cifras de nuestro sistema decimal, cuantos números diferentes de 4 cifras (repetidas o no) se pueden formar?
4. Permutaciones ordinarias
Imagínate que vas al cine con 5 amigos. Os sentáis en seis butacas consecutivas de una fila. ¿De cuantas formas distintas os podéis sentar?
Aprende más sobre ...
De 720 maneras diferentes! Sorprendente, no?
En el primer asiento se pueden sentar 6 personas, 5 en el segundo, 4 en el tercero, etc. Matemáticamente hay 6·5·4·3·2·1= 720 posibilidades. Esto se representa con el 6 factorial (6!)
En las permutaciones intervienen todos los elementos y sólo varía el orden de colocación.
Y ahora, ¿Sabrías decir de cuántas formas se pueden alinear 10 cartas de una baraja? No te asustes si te sale un número millonario
Un caso particular son las permutaciones circulares.
Después del cine, os vais a cenar, pero la mesa es circular. Ya no hay tantas posibilidades, es normal. De un plumazo nos cargamos 600 posibles opciones. Cómo me gustan los círculos!!
Cuando la permutación sea circular, reducimos en 1 el número de elementos. En este caso se reduce a 5!=5·4·3·2·1 = 120 En general, tenemos que:
Es bien sabido que la disposición de los comensales en una mesa puede plantear problemas más interesantes de lo que puede parecer a primera vista.
5. Permutaciones con repetición
Un jugador de ajedrez quiere ordenar en una fila 5 peones negros y 3 peones blancos. ¿De cuántas formas distintas podrá hacerlo?
En este caso los elementos están repetidos. Se trata de una permutación de 8 objetos donde 5 están repetidos, y tres están repetidos. En estas ocasiones podemos expresarlo así:
Si comprendes lo que te pide el problema, entenderás la fórmula anterior. Pero por si acaso, aquí tienes la fórmula general para resolver cualquier problema de permutaciones con repetición.
6. Combinaciones ordinarias. Combinatoria pura
Noticia! En las combinaciones no importa el orden!!
Por este motivo NO puedes decir “¿sabes la combinación del candado?”
Combinaciones ordinarias o sin repetición de m elementos tomados de n en n (n≤m), son los distintos grupos que se pueden formar de tal forma que:
- En cada grupo entre n elementos distintos
- Dos grupos serán diferentes si difieren en algún elemento, pero no en el orden de colocación
Aquí ya aparecen los números combinatorios, los mismos que surgen en el fantástico triángulo de Pascal. En general, siempre se cumple que:

En una clase de 30 alumnos, queremos escoger una comisión de 5 alumnos. ¿De cuántas formas diferentes se puede hacer?
No son pocas. ¿Te salen 142506? Bien!!
7. Combinaciones con repetición
El último caso es similar al anterior. Pero ahora es posible repetir los elementos.
Por ejemplo: ¿Cuántos helados diferentes de dos bolas se pueden formar con los 10 sabores que hay en una heladería?
El orden no influye. Puede haber repeticiones (yo nunca repito ;-))
Se trata por tanto de combinaciones con repetición de 10 elementos tomados de 2 en 2. Al haber repetición, en matemáticas se expresa de esta forma:
CR m , n = C m+n-1 , n
En nuestro problema nos quedaría así:
Cómo no vamos a ser tan indecisos, si tenemos 55 helados diferentes para elegir …
Variaciones permutaciones y combinaciones
La combinatoria es una rama de las matemáticas que se encarga de estudiar los diferentes arreglos y agrupaciones que se pueden hacer con un conjunto de elementos. Para esto, como acabamos de ver, se utilizan tres conceptos fundamentales: variaciones, permutaciones y combinaciones.
Las variaciones son agrupaciones ordenadas de elementos tomados de un conjunto. Es decir, se toman algunos elementos y se ordenan de diferentes maneras. Por ejemplo, si tenemos los números 1, 2 y 3, las variaciones de 2 elementos serían (1, 2), (1, 3), (2, 1), (2, 3), (3, 1) y (3, 2). La fórmula para calcular las variaciones es n!/(n-k)!, donde n es el número total de elementos y k es el número de elementos que se toman.
Las permutaciones, por otro lado, son agrupaciones de elementos en las que el orden sí importa, pero se toman todos los elementos del conjunto. Por ejemplo, si tenemos los números 1, 2 y 3, las permutaciones serían (1, 2, 3), (1, 3, 2), (2, 1, 3), (2, 3, 1), (3, 1, 2) y (3, 2, 1). La fórmula para calcular las permutaciones es n!, donde n es el número total de elementos.
Por último, las combinaciones son agrupaciones en las que el orden no importa y se toman solo algunos elementos del conjunto. Por ejemplo, si tenemos los números 1, 2 y 3, las combinaciones de 2 elementos serían (1, 2), (1, 3) y (2, 3). La fórmula para calcular las combinaciones es n!/((n-k)!k!), donde n es el número total de elementos y k es el número de elementos que se toman.
Estas fórmulas de combinaciones, permutaciones y variaciones son muy útiles para resolver problemas de probabilidad, estadística y análisis combinatorio. Además, nos permiten calcular de manera precisa la cantidad de posibilidades que existen al realizar diferentes arreglos y agrupaciones con un conjunto de elementos dado. Así, la combinatoria se convierte en una herramienta esencial en el estudio y desarrollo de diversas áreas de las matemáticas y la ciencia en general.
Tal vez te preguntes, que fórmula debo emplear en cada caso. Todo dependerá de cuál sea el enunciado. Cómo resumen, aquí te dejo un mapa mental para “descubrir” la solución a tu problema.
Esquema de combinatoria. Mapa mental
Espero que este esquema de combinatoria te haya sido útil, y que hayas podido recordar o aprender un poco de matemáticas.
Ahora ya puedes pensar, y preguntarte todo lo que quieras. Realmente la combinatoria no es tan dificil como las pintan. Las matemáticas siempre estarán ahí, con los brazos abiertos, para que encuentres la solución a tus preguntas.
Me gustaría mucho que aportaras tus dudas o comentarios, aprenderemos todos. ¡Un abrazo!
Aprende más sobre ...
Espero que te haya gustado este artículo sobre Combinatoria: Variaciones, permutaciones y combinaciones. Fórmulas. Me ayudarás mucho si lo compartes en tus redes sociales. Debajo tienes los botones🎯¡Hasta pronto!
-
Excelente la explicación de la combinatoria, resumido, bien explicado, no quedó nada en el tintero.
-
Muchísimas gracias. Comentarios como el tuyo me cargan las pilas.
Un abrazo!
-
-
Mucho mejor después de leer el artículo 😘
-
Genial! Gracias 😉
-
-
Hooa buenas, ¿me pueden ayudar con un problema? Por favor y gracias; dice así el problema: a Juan le regalan una coleccion de muñecos de plastico de superhéroes, entre los que se encuentran 3 hombres y 4 mujeres. Si él los quiere poner en su repisa en una fila, el número de maneras en que lo puede hacer de forma que haya un hombre y una mujer alternadamente es: A.144 (creo que esta es porque 4!3! da eso) B.64 C.72 D.121
-
TENGO UN GRUPO DE 73 FICHAS QUE HAN DE TENER DURANTE 18 DIAS UN NUMERO DE UNA DETERMINADA ZONA (SON 10 ZONAS).
-
Holiiiiiiiiis
Mañana me podrias ayudar en unos es q tengo dudas, pliis -
Holaaaa me podrías ayudar con este:
a) ¿Cuántas elecciones distintas de delegado(a) y subdelegado(a) se pueden
realizar en una clase de 25 alumnos(as)?
b) ¿Cuántas si de los 25 hay 15 alumnas y 10 alumnos e imponemos la
condición de que delegado(a) y subdelegado(a) sean de distinto sexo? -
¿De cuántas maneras diferentes se pueden sentar 4 varones y 3 mujeres en una banca de 7 asientos de tal forma que las mujeres siempre se sienten juntas?
-
Álvaro y sus 5 amigos se sientan en una mesa circular. ¿De cuántas maneras diferentes se pueden ubicar?
-
Se trata de una permutación circular, siendo PCn=(n-1)! En este caso, al ser 5 amigos sentado en la mesa circular, será 4!=24 maneras diferentes.
Si lees con calma el artículo, podrás contestar las demás preguntas. O tal vez algún lector.
Saludos!
-
-
Con los dígitos 1;3;4 y 9, ¿Cuántos números distintos de 4 cifras se pueden formar?
-
En una competencia de atletismo participan 9 atletas. ¿De cuántas maneras diferentes pueden ocupar los tres primeros lugares?
-
En Colombia las placas de los carros están formadas por tres números y tres letras.
eniendo en cuanta lo anterior, determinar:
1. ¿Cuántas placas se pueden generar en estas
condiciones?
2. ¿en este experimento es válido hablar del orden en la muestra? ¿es válido hablar de
la repetición en la muestra? Justificar la respuesta.
3. En el caso que para una ciudad como Medellín se asignen solamente las placas cuya
primera letra es M o N, ¿Cuántos automóviles pueden estar matriculados en Medellín?
4. La medida del pico y placa ha sido una alternativa para solucionar el problema de sobre
circulación de vehículos en las horas en las cuales el trafico es muy complicado.
Suponiendo que el día miércoles tiene pico y placa todos los vehículos del país cuya
placa termina en 1 y 2. ¿Cuántos vehículos podrían estar circulando este día?
5. Con esta medida, ¿Cuántos vehículos circularían en Medellín el día miércoles? -
Hola buenas noches, podrán ayudarme con el siguiente problema?
* Cuantas claves se pueden formar al generar una reunión en la app Zoom?Gracias!!
-
Hola Julieta. Desconozco el número de casillas o posibilidades que ofrece esta herramienta para generar una reunión.
¿Puedes darme más datos? Gracias
-
-
hola Profesor , me podria ayudar con este problema .De cuantas maneras se pueden ubicar 5 autos en fila en un estacionamiento sus colores son verde, azul, rojo, negro y blanco? ¿Cuáles son? gracias
-
Diana, siento la tardanza en contestar.
Tienes que darte cuenta que intervienen todos los elementos y no repite ninguno. Por tanto se trata de una permutación de 5 elementos.
Es decir 5!=5·4·3·2·1=120 posibilidades
Saludos-
Hola me podrían colaborar con este ejercicio con las 10 cifras de nuestro sistema decimal cuantos numero diferentes de 4 cifras se pueden formar?
-
Disculpa por contestar tan tarde. En el comienzo de curso voy muy liado.
Se trata de variaciones con repetición. En el artículo lo entenderás bien. VR10,4= 10^4=10000 cifras.
Saludos!
-
-
-
-
En la pregunta incorporé un error. Debe decir "Con los dígitos {0, 1,…,9} deseo formar números de siete dígitos que no empiecen ni por 0 ni por 1."
-
Gracias por la aclaración Enrique. Bonito problema de combinatoria.
Muy buena explicación la que has dado. El razonamiento y la resolución es correcta.
¡Saludos!
-
-
Estimado Justo, te agradeceré me orientes en el siguiente problema.
Con los dígitos {0, 1,...,9} deseo formar números de cinco dígitos que no empiecen ni por 0 ni por 1.
¿Cuántos números podemos formar que contengan una subcadena de 5 dígitos consecutivos?.
Yo razono lo siguiente.
Cadenas con 5 dígitos consecutivos tenemos {01234, 12345, 23456, 34567, 45678, 56789}, seis posibilidades.
Cadenas con 5 dígitos consecutivos que no empiecen por 0 ni por 1 tenemos {23456, 34567, 45678, 56789} hay cuatro.
Cadenas que puedo formar que empiecen con cuatro dígitos consecutivos es 4 x VR_10² = 400.
Con cuatro dígitos consecutivos en el centro tendremos 8 x 6 x 10 (no pueden empezar por 0 ni 1 y pueden finalizar con cualquier dígito). 480
Con cuatro consecutivos al final 8 x 10 x 6 = 480
Total 480 + 480 + 400 = 1360
¿Es correcto mi razonamiento.
Saludos cordiales
-
Hola, me podría ayudar con este ejercicio:
De cuántas maneras pueden ser contratados siete maestros de matemáticas de entre 10 maestros y 7 maestras, si:
a) 3 maestros y 4 maestras.
b) 5 maestras y 2 maestros.-
10C3 * 7C4 = 120 * 35 = 4200
10C2 * 7C5 = 45* 21 = 945
-
-
hola profe muy buena esta explicacion, profe me puede ayudar con algunas preguntas que me pusieron y no entiendo, muchas gracias.
- se presenta a un banco 6 aspirantes para lograr uno de los cuatro puestos disponibles para laboral. ellos son: diego, felipe, guillermo, hugo, ivan y jorge de cuantas y cuales maneras diferentes- escribe las - pueden escogerse los o candidatos?
- cuantos números de cuatro se pueden formar con los numeros digitos, si
a) los números pueden repetirse hasta dos veces
b) los números pueden repetirse hasta tres veces
muchas gracias-
Muchas gracias Andrea. Me alegro que te haya gustado.
- En los 6 aspirantes no importa el orden. Por tanto, usaremos combinaciones C(6,4)=30 Pon letras para aclarate a ponerlas todas DFGHIJ
- En el caso de los dígitos (supongo 10, del 0 al 9) iimporta el orden e intervienen todos los elementos. Por lo que se trata de permutaciones con repetición (revisa el artículo y lo entenderás mejor)
a) si pueden repetirse dos veces haremos P= 10!/4!2! que da un valor de 75600 números. El b) te lo dejo para tí 😉
Un abrazo!
-
-
Me gustaría que me dieras la respuesta del el ejercicio planteado:"¿ cuántos números de 4 cifras se pueden representar con los 10 dígitos (repetidos o no)?"
Gracias-
Hola Nicolás,
¿Cuántos números de 4 cifras se pueden representar con los 10 dígitos sin repetir?
Imagínate que tienes 4 huecos o cajas vacías, la primera puedes poner un número de 0 al 9 (es decir, 10 dígitos posibles), en la segunda 9, ...
Se trata de variaciones de 10 elementos tomados en 4 posiciones: por tanto 10*9*8*7=5.040 númerosSi se pueden repetir, son variaciones con repetición VR 10,4 = 10^4= 10.000 posibilidades
Saludos!
-
pero Fernández, que pasa con el 0 si le pones como posibilidad en la primera cifra, en ese caso se formaria 3 cifras, emtonces no seria 9 dígitos? o me equivoco
-
Gracias por comentar.
Según las consideraciones que se hagan. Yo he supuesto que el 0785 es un número de cuatro cifras igual de válido (en un candado por ejemplo) que el 0000
Saludos!
-
-
-
-
Una síntesis muy trabajada (eso es una consecuencia de la experiencia)´Muchas gracias.
-
Me alegro que te haya gustado Daniel.
Gracias a tí. Saludos!
-
-
Posibles clasificaciones de ocho equipos que juegab en una liga y tienen k enfrentarse entre todos, y en cuantas de ella un equipo A quedaría entre los tres primeros.
-
Hola Valerio.
Al influir el orden y no haber elementos repetidos, se trata de variaciones de 8 elementos tomados de 3 en 3.
V(8,3)=8·7·6=336 posibilidades
Saludos
-
-
Buenos días, me podrían explicar por favor la verdad no entiendo de donde sale los 720. muchas gracias desde ya.
-
Hola Ediza.
Simplemente hay que aplicar la combinatoria. Si fueran 2 personas, solo caben dos posibilidades (2·1=2). Si van 3 (3·2·1= 6 posibilidades) y así sucesivamente. Se trata de permutaciones)
En las permutaciones intervienen todos los elementos y sólo varía el orden de colocación.Saludos!!
-
-
¿Cuál es la sencilla fórmula algebraica para la elaboración de la cantidad de combinaciones en base a los siguientes criterios?
combinaciones = n elegir r (por ejemplo, 50 bolas y elige 5 bolas)
filtered_1_combinations = combinaciones quitan donde R tiene los números de x1, x2, x3, x4, x5, x6 (p. ej., 1,5,12,24,44,45) filter_2_combinations
= eliminar combinaciones de filter_1_combinations donde las combinaciones tienen más de 2 números de probabilidad
filter_3_combinations = eliminar combinaciones de filter_2_combinations donde las combinaciones tienen entre y1 e y2 números consecutivos (por ejemplo, si y1 = 1 e y2 = 3, entonces una combinación aceptada es 1,2,3,5,7 pero no 1,2,3,4,7 ) -
Hola me podrían ayudar con un problema porfavor:
-En un restaurante ofrecen a sus clientes la posibilidad de armar las ensaladas a su gusto.Cada ensalada puede llevar dos proteínas y dos aderezos, si el restaurante dispone de 5 tipos diferentes de proteínas y 4 aderezos en los que puede elegir,¿Cuántas ensaladas diferentes se pueden preparar?
A.20
B.24
C.48
D.60-
Hola Madeleine!
Aplicando el principio de multiplicación, tenemos que 5*4=20 ensaladas diferentes.
Saludos-
Hola,
Creo que 20 sería la solución si solo pudiese llevar 1 aderezo y 1 proteína, pero en el enunciado dice que puede llevar 2 aderezos y 2 proteínas, así que no es la solución.
Un saludo -
Justo, no leíste bien el problema, no es usando todos los aderezos y todas las proteínas; es usando sólo 2 aderezos y sólo dos proteínas. o sea, cada resultado será de la forma (A1,A2, P1,P2); (A1,A2,P1,P3)....(A3,A4,P4,P5) En total 60 combinaciones posibles
-
Gracias por decírmelo y revisarlo. Tengo la cabeza en muchos sitios 😉
Saludos!
-
-
-
En ese caso, yo creo que tienes que calcular cuántas formas de elegir dos proteínas entre 5 (combinación sin repetición, aunque no dice si puedes elegir dos de la misma proteína) y multiplicarlo por la cantidad de formas de elegir dos aderezos entre 4, ya que cada combinación de proteínas la puedes juntar con cada combinación de aderezos...sería 10 x 6 = 60
-
-
Imagínate que vas al cine con 5 amigos. Os sentáis en seis butacas consecutivas de una fila. ¿De cuantas formas distintas os podéis sentar?
De 720 maneras diferentes! Sorprendente, no?
En el primer asiento se pueden sentar 6 personas, 5 en el segundo, 4 en el tercero, etc. Matemáticamente hay 6·5·4·3·2·1= 720 posibilidades. Esto se representa con el 6 factorial (6!)
Xq es factorial de 6 si solo son 5 amigos
-
Hola Cristian. Es cierto que puede llevar a confusión, pero dice si vas (tú) al cine con 5 amigos, es decir 1+5=6
Gracias por comentar. Saludos!
-
Hola. Para empezar, maravilloso el blog.
Yo entendi lo mismo: que iban solo cinco personas al cine y se reparten en seis butacas.
En el caso de que fuesen cinco personas al cine y se sentasen en 6 butacas, para mi se resolveria de la misma forma: juego con el espacio en blanco donde no se sienta nadie. Tambien lo pongo como factor (como si fuese un amigo mas: un espacio entre dos de los amigos o al principio o al final). Es decir, el resultado vendria a ser el mismo.
Seria correcto?
Gracias por los aportes-
Muchas gracias por tus palabras!
Fíjate que en el artículo sice: "Imagínate que vas al cine con 5 amigos",es decir, contándote a tí, sois 6.
Cierto, si consideramos a un amigo invisible, sería lo mismo.
Un abrazo!
-
-
-
-
Muchas muchas muchas gracias, me re ayudaste con un punto o dos del parcial, 10/10 ♡
-
Me alegro que te haya servido! Pero tienes que darte las gracias a tí misma por haber puesto el interés necesario para aprender ...
Saludos!
-
-
EXCELENTE
GRACIAS POR COMPARTIR
-
Me alegra mucho que te haya gustado.Gracias a tí.
Un abrazo!
-
Me parece muy interesante y bien planteado y claro. Gracias.
-
Muchas gracias por tus palabras!!
-
Excelente página. Saludos desde Bolivia!
-
-
-
-
55 lectores opinan:
Deja una respuesta



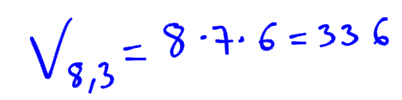

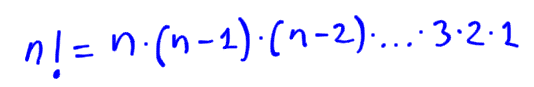
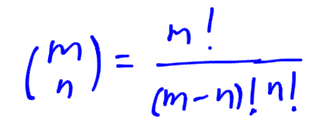


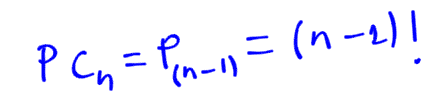

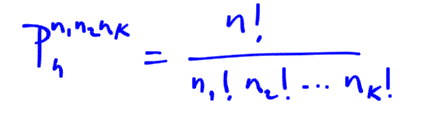
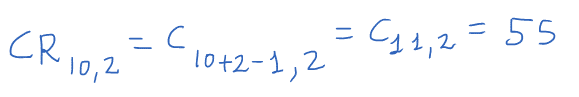




Quiero aprender más sobre: