Lejos, muy lejos están de saber cuál es el área del círculo. Ni siquiera me conocen.
Acabo de nacer, mis constantes vitales (centro y radio) están bien. Pero todavía no han descubierto mi constante universal, esa que regirá el mundo. ¡Qué sorpresa se van a llevar!
Nacimiento del círculo
Me encuentro en la Grecia clásica, donde las palabras matemático y geómetra vienen a ser lo mismo. Les oigo dialogar, se encuentran maravillados por mi belleza y elegancia. Mi abrumadora sencillez les sorprende. Nadie sabe cuál es el área del círculo, todavía no me conocen.
Sé que en poco tiempo me convertiré en uno de los conceptos geométricos más importantes. Estoy dotado de una autentica perfección en dos dimensiones. (Perdón por mi chulería).
Tengo un defecto, soy plano. Pero una gran virtud: mi radio de acción es brutal, porque todos mis puntos están a la misma distancia de mi centro.
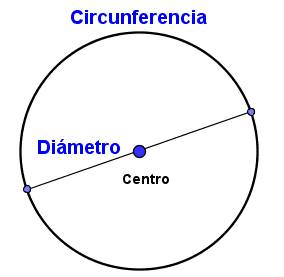
Me dividen infinitos diámetros ansiosos por tocar mi centro.
No me confundáis con la circunferencia. Ella es parte de mí. En la lejanía, desde mi centro, diviso una curva continua que me cierra el paso, de la que no puedo salir. Es mi circunferencia.
Ehh! Están hablando de mí. Ahora los matemáticos dicen que todos los círculos son semejantes. ¿Te parece poca cosa? No todos los triángulos tienen la misma forma, ni los rectángulos, y no hablemos de las “irregularidades” de las personas … Seamos grandes o pequeños, todos tenemos la misma forma. Nuestra redondez perfecta es evidente.
Silencio! Ahora han dicho algo importante. Lo acaban de descubrir. Una verdad que perdurará en el devenir de los tiempos. Uno de los teoremas más profundos de las matemáticas: la razón de la circunferencia al diámetro es la misma para cualquier círculo. No importa el tamaño! Aquí tampoco! Aunque sea un círculo gigantesco o uno minúsculo, el tamaño relativo de la circunferencia (C) al diámetro (D) será exactamente el mismo.

¿Cómo le llamaran a esta constante?
Creo que han escogido bien. Mi constante vital se llamará Π, la decimosexta letra del alfabeto griego. Bonito símbolo, una clase de inmortalidad matemática.
Este símbolo fue adoptado por William Jones en 1706 y popularizado por el genio matemático Leonhard Euler.
Caracterización del círculo
Con el paso de los años los matemáticos me han estudiado bien. Han dejado bien claro quien soy. Me tienen fichado. Mira lo que dicen sobre mí ...
Si C es la circunferencia de un círculo y D es su diámetro, siempre se cumple que:

De esta forma π suministra una conexión crítica entre 2 longitudes: la circunferencia y el radio.
Es muy importante, aunque no parece claro desde un punto de vista intuitivo, que la constante π conecta igualmente bien el área y el radio del círculo.
Área del círculo ¿Cómo han podido conocerme tan bien?
Para empezar, han tenido que aproximarme a un polígono regular (de lados y ángulos iguales).
Aprende más sobre ...
Los polígonos son figuras más accesibles que los círculos.
En la siguiente figura puedes ver un pentágono regular inscrito en un círculo de radio r. Para determinar el área del pentágono, me trazan radios desde el centro del círculo a los cinco vértices sobre el círculo, dividiendo el pentágono en cinco triángulos.
Cada triángulo tiene de base la longitud b, el lado del pentágono, y de altura h, la línea discontinua perpendicular trazada desde el centro del círculo hasta el lado del polígono y que se llama apotema.
Conociendo el área de un triángulo, observan que:

Y por tanto:

Pronto observan que la misma fórmula es válida si se inscribe en un círculo un polígono regular de 10 ó 50 lados. Para el caso general de un polígono regular con n lados, tendremos n triangulitos. Ya que el perímetro es n veces la longitud b de cada lado.
El área del círculo está cerca de ser descubierta.
De manera intuitiva observan que aumentando el número de lados del polígono regular, irán “rellenando” gradualmente el círculo. Y las áreas de las figuras inscritas se aproximarán al área del círculo como a un límite superior.
Área del círculo = límite del área de los polígonos regulares inscritos = límite [(1/2)h · perímetro]
No podrán alcanzarme. Por más que incrementen su número de lados, los polígonos regulares inscritos en mí, no llegarán nunca a mi exquisita redondez. Aunque la aproximación es muy buena.
¿Qué le pasa a la apotema y al perímetro cuando el número de lados de un polígono aumenta indefinidamente?
Claramente, h tendrá como límite el radio del círculo. También es fácil intuir que el límite del perímetro es igual a la longitud de la circunferncia (C).
De ahí que:

Por fin llegamos a determinar el área del círculo. Recordando la primera ecuación donde aparecía π, la fórmula anterior se convierte en:

Ésta es sin duda, una de las fórmulas clave de todas las matemáticas.
Termino con estas letras de un libro muy recomendable que acabo de volver a leer La historia interminable: "Todo se mueve en círculos. Lo que aparece debe desaparecer y lo que nace debe morir"
Te acordarás de mí, porque me verás por todas partes.
Aprende más sobre ...
Hasta pronto ...
Espero que te haya gustado este artículo sobre Obtención del área del círculo. Me ayudarás mucho si lo compartes en tus redes sociales. Debajo tienes los botones🎯¡Hasta pronto!
-
-
Hola Juan Miguel!
Muchas gracias por tus palabras y tu aportación. Yo también me pregunto lo mismo, y estoy de acuerdo contigo. Por cierto, hoy mismo he publicado un artículo sobre el número PI ...
Un abrazo!
-
-
no entendi nada
-
Hola,
Trato de hacer una visión histórica de la importancia del círculo y el misterio de PI.
Siempre se cumple que el cociente entre la longitud de la circunferencia y el diámetro de esta siempre es el mismo, el infinito número PI.
Espero que leyéndolo con más calma puedas entenderlo. Saludos!
-
-
Pi el numero perfecto en el circulo, ya que sin este numero no se podria resolver enigmas ni misterios................
-
Gracias por tu aportación.
El número pi siempre a fascinado a la humanidad.Matemáticos de todas las épocas han dedicado parte de sus vidas a obtener alguno de sus dígitos. Pi es un número irracional e infinito. No valen aproximaciones,el valor verdadero de pi se pierde siempre en la inmensidad del infinito.Saludos 😉
-
Excelente tu artículo. Me gusta.
Sin embargo te hago notar algunos problemillas :
"a fascinado" debe ser "ha fascinado"¿A que llamas un número infinito? Tal vez debería decirse "con cantidad infinita de dígitos, es decir un número irracional".
-
Muchas gracias Fernando. Enseguida corrijo el error ortográfico.
Cierto. Además de cualquier número irracional, también podemos decir que hay números naturales infinitos, por ejemplo el número de granos de arena de la playa o el número de estrellas que hay en el universo.
Un abrazo.
-
-
-
8 lectores opinan:
Deja una respuesta



Estimado Justo:
El artículo es interesante, sencillo, divertido y, sobre todo, práctico. Sin embargo siempre me he preguntado cómo los antiguos llegaron a la conclusión de que, efectivamente, el cociente entre la longitud de una circunferencia y su diámetro era una constante que más tarde se le dio el nombre de Pi. Yo imagino que durante siglos la única manera de llegar a esa conclusión fue midiendo. Y, luego, comprobando que los resultados de diferentes matemáticos, de diferentes pueblos y épocas, eran los mismos trataron por distintas vías de construir una demostración de carácter universal o analítica. En todo caso, esta simplísima y casi mágica relación es sorprendente y maravillosa. Un cordial saludo.