Cómo calcular el dominio de una función. Ejercicios

¿Entiendes bien qué es el dominio de una función? Suele causar problemas a los estudiantes.

Tienes que saber que el dominio de una función es fundamental en el estudio de representaciones gráficas.

Cómo hallar el dominio de una función

En este artículo te lo explico con todo detalle, para que no tengas ninguna duda.

Conceptos básicos de funciones

Las relaciones entre magnitudes son descritas de forma elegante y práctica mediante el lenguaje de las funciones. Hay muchos tipos de funciones (lineales,cuadráticas,exponenciales…) que nos ayudan a estudiar una variedad infinita de situaciones reales. Aunque no te lo creas, todos los días utilizas funciones. Sin lugar a dudas el concepto más importante de todas las matemáticas es el de función. Las funciones pueden venir dadas de varias formas: por su gráfica, mediante una tabla de valores, por una fórmula o a través de una descripción verbal.

Siempre me he imaginado una función como una máquina donde entran unos números y salen otros. Aunque no siempre es así 😉

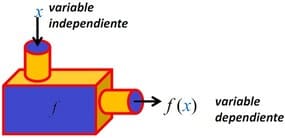
Una función liga dos variables numéricas, habitualmente llamadas x e y

x es la variable independiente (la que entra), y es la variable dependiente (la que sale)

Nuestra máquina de hacer números o función se suele denotar por y=f(x). Relaciona cada valor de x con un único valor de y:

En la siguiente imagen puedes ves un ejemplo sencillo, de como varia f(x) según los valores de x.

Pero debes estar atento. En muchas ocasiones para un valor determinado de x, no le corresponde ningún valor de f(x).

Entonces, ¿qué pasa si no le corresponde ningún valor de f(x)? Muy sencillo, para ese valor de x, la función f(x) no existirá. Dicho de otra forma, “la máquina se rompe”

Por ejemplo, a la función  \(y=frac { 2 }{ x }\), no podemos asignarle el valor cero, porque es imposible dividir entre cero. Es decir, para x=0 esta función no existe

Antes de ver en que casos puedes encontrarte estas situaciones, es coveniente que sepas identificar fácilmente el dominio viendo la gráfica de la función.

¿Cómo puedo identificar el dominio de una función en una gráfica?

Esto es muy sencillo, no te preocupes. Además hoy en día hay herramientas fabulosas como Desmos, que te permiten representar funciones fácilmente.

En los siguientes ejemplos lo verás fácilmente. La función viene representada en color azul y el dominio en color verde. Se aprecia con claridad que el dominio de una función son todos los valores de la variable x que tienen una imagen, es decir, en su misma vertical aparece un valor de la función representada, f(x) existe.

Ten en cuenta que para ver el dominio siempre debes mirar en el eje X.  Enseguida podrás ver si hay algún valor que no pertenezca al dominio de función. Te pongo dos ejemplos:

Dominio de una función. Ejemplos

Se llama dominio de una función f, escrito \(Domf\) , al conjunto de valores de x para los cuales existe la función, es decir, para los cuales hay un f(x).

Buscar valores que no pertenezcan al dominio. Cuándo la función no existe

Siempre resulta interesante encontrar (si los hay) estos casos. Debes ser capaz de ver que operaciones tienes que hacer para encontrar los valores que no tienen imagen, que hacen que la función no exista. Estos son los casos más comunes:

 1. Es imposible dividir entre cero

Es una operación prohibida en matemáticas. ¿Cómo puedes dividir 10€ entre nadie? Nunca podrás dividir entre cero.

Por ejemplo, si  \(y=frac { 5{ x }^{ 2 }-3 }{ x }\) , esta función no está definida para x=0

2. El radicando de una raíz de índice par no puede ser negativo

\(sqrt { -7 } rightarrow\) no existe                     \(sqrt [ 4 ]{ -5 } rightarrow\) existe

3. El logaritmo de cero o de un número negativo no existe

\(log(0)rightarrow\) no existe                               \(log(-7)rightarrow\)no existe

Es muy importante que sepas buscar los valores para los cuales una función no existe. Veamos dos ejemplos prácticos:

#Hallar el dominio de    \(y=frac { 1 }{ { x }^{ 2 }-2x-8 }\)

Enseguida te debes dar cuenta que el denominador no puede ser cero. Por tanto, hay que buscar los valores malditos que rompen la máquina. ¡A por ellos!

\({ x }^{ 2 }-2x-8=0quad rightarrow quad x=frac { 2pm sqrt { 4+32 }  }{ 2 } =frac { 2pm 6 }{ 2 } =4quad yquad -2\)

Por tanto, acabas de ver que los valores x=–2 y x=4 anulan el denominador, por lo que no pertenecen al dominio de definición. En este caso \(Domquad f=Re -left{ -2,4 right}\)

# Hallar el dominio de   \(y=sqrt { x+3 }\)

¿Y ahora qué? La raíz no puede ser negativa.

Es decir \(x+3ge 0quad rightarrow quad xge -3\)

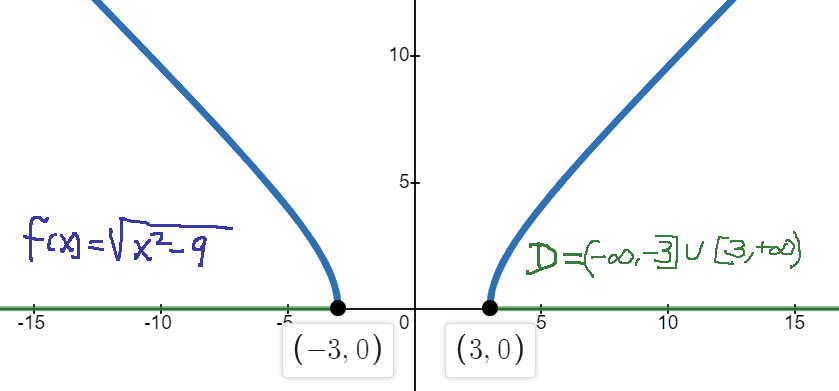
En la gráfica puedes observar que el dominio existe desde –3 hasta el infinito, esto lo expresamos así:  \(Domquad f=left[ -3,+infty  right)\)

El concepto de dominio de función no resulta fácil de entender para algunos alumnos, pero es más fácil de lo que parece. La clave principal es encontrar los valores para los cuales la función no existe. Ya que todos los demás valores pertenecerán al dominio de la función.

Aprende más sobre ... Sistemas de ecuaciones no lineales

Lo más conveniente es estudiar el dominio de las funciones más importantes que te puedes encontrar. Pero antes puedes ver a las funciones bailando en el siguiente video. Mola.

Cómo hallar el dominio de las funciones más importantes. 

* Dominio de una función polinómica

Suelen ser las favoritas de cualquier estudiante porque no dan ningún problema. Su dominio es el valor de todos los números reales. En ellas no te encontrarás raíces ni denominadores que te compliquen la vida. Ejemplo:

\(f(x)={ x }^{ 3 }+5{ x }^{ 2 }-1\)

Dicho de otro modo, en las funciones polinómicas no hay valores de x para los cuales no exista f(x), es decir, la función siempre existirá. Decimos entonces que su dominio es el conjunto de todos los números reales:

\(Domquad f=Re\)

* Dominio de una función racional

El dominio de estas funciones será R, excepto los valores que anulan el denominador. En estos casos, para obtener el dominio de una función racional, tienes que buscar el valor o los valores que hacen cero el denominador. Estos valores no pertenecerán al dominio. Antes has podido ver un ejercicio resuelto. Te muestro un ejemplo más:

\(f(x)=frac { 3 }{ x-7 }\)    \(Domquad f=left{ Re -7 right}\)

Es decir, la función existirá siempre que x sea distinto de 7, por tanto el dominio es el conjunto de todos los reales menos el número primo 7

* Calcular el dominio de una función irracional

¿Qué es una función irracional? Es aquella en la que aparece una raíz. Porque las raíces no pueden ponerse en forma racional o de fracción. El mismísimo Pitágoras lo pasó muy mal con esto.

Aquí resulta preciso distinguir entre dos casos diferenciados.

• Raíces de índice impar. Siempre existen. Su dominio es R
• Raíces de índice par. Existirán siempre que su radicando sea igual o mayor que cero

Ejemplos:

\(f(x)=sqrt { x-5 }\)  Como es una raíz de índice par, existirá siempre que su radicando sea mayor o igual que cero. Entonces:

\(x-5>0quad rightarrow x>5\)\(Domquad f=left[ 5,+infty  right)\)

\(f(x)=sqrt [ 3 ]{ { x }^{ 2 }+5 }\)

En este caso puedes ver que la raíz es de índice impar, por tanto siempre existirá. Su dominio de función será        \(Domquad f=Re\)

* Dominio de una función logarítmica

Recuerda que las funciones logarítmicas son las que contienen a la x dentro de un logaritmo.

Estas funciones siempre existirán cuando el logaritmo sea mayor que 0. Esto es lo que tienes que buscar. Los otros valores, serán los que hacen que el logaritmo sea cero o negativo. Y estos valores los que tienes que excluir del dominio de la función. Veamos:

\(f(x)=log { left( x-9 right)  }\)

Siempre y cuando el logaritmo sea mayor que cero, esta función existirá:

\(x-9>0quad rightarrow quad x>9\)

Entonces queda claro que la función existirá cuando x sea mayor que 9. Es decir, su dominio será:

\(Domquad f=(9,infty )\)

El paréntesis indica que 9 no pertenece al dominio, porque si x=9, obtenemos logaritmo de cero, y esto no existe.

* Como calcular el dominio de una función exponencial

Las funciones exponenciales son las que tienen la x en el exponente. Como base puedes tener cualquier número real mayor que 0 y distinto de 1. Lo expresamos de esta forma:

\(f(x)={ a }^{ x }quad conquad aneq 1quad yquad a>0\)

Ejemplos de estas funciones tan particulares hay infinitos. El numero e suele jugar un papel importante.

\(f(x)={ 3 }^{ x }quad quad quad quad f(x)={ e }^{ { x }^{ 2 }+5x }\)

Y ahora te pregunto, ¿ves algún valor de x que haga que estas funciones no existan? Yo tampoco. En consecuencia, el dominio de estas funciones será el conjunto de todos los números reales. Esta función, como las polinómicas, siempre existe.

\(Domquad f=Re\)

Si lo prefieres, puedes ver el siguiente vídeo para consolidar lo aprendido.

Ejercicios de dominios de funciones

¿Te atreves con estos ejercicios? Ahora te toca a tí encontrar el dominio de las siguientes funciones, algunas sencillas y otras más complejas. En el aprendizaje de las matemáticas es muy importante razonar y practicar mucho, esa es la clave del éxito. A ver si eres capaz de resolver estos ejercicios:

1) \(f(x)=frac { 2 }{ 2x+4 }\)

2) \(f(x)=frac { 1-x }{ { x }^{ 2 }-x-6 }\)

3) \(f(x)=sqrt { -{ x }^{ 2 }+2x+3 }\)

4) \(log { ({ x }^{ 2 }+6x) }\)

Soluciones

1) \(Domf=left{ Re -left( -2 right) right}\)

2)  \(Domf=left{ Re -left( -2,3 right) right}\)

3) \(Domf=left[ -1,3 right]\)

4) \(Domf=left( -infty ,-6 right) cup left( 0,+infty right)\)

¿Te ha gustado la entrada? Espero que te haya podido ayudar. Es importante que no te dominen las funciones ;-)Si te has quedado con dudas, puedes ver el vídeo con los ejercicios de dominio de funciones resueltos. No dejes de explorar tus dominios

Aprende más sobre ... Cómo multiplicar matrices de forma fácil y rápi...

Te agradecería mucho que me comentaras cualquier inquietud o sugerencia. Si ienes alguna duda, indícalo en los comentarios y te ayudaremos.

Como encontrar el dominio de una funcion

Tipo de Función	Descripción	Consideraciones para el Dominio
Funciones Polinómicas	Funciones definidas por un polinomio de la forma (a_nx^n + a_{n-1}x^{n-1} + ldots + a_1x + a_0).	El dominio es todos los números reales ((mathbb{R})), ya que se pueden evaluar en cualquier valor real de (x).
Funciones Racionales	Funciones que son el cociente de dos polinomios, de la forma (frac{p(x)}{q(x)}), donde (q(x) neq 0).	El dominio excluye los valores que hacen que el denominador sea cero. Se deben encontrar las raíces de (q(x)) y excluirlos del dominio.
Funciones Radicales	Funciones que contienen una raíz cuadrada, cúbica, etc., de la forma (sqrt[n]{f(x)}).	Para raíces pares, el argumento debe ser mayor o igual a cero ((f(x) geq 0)). Para raíces impares, el argumento puede ser cualquier número real.
Funciones Logarítmicas	Funciones de la forma ( log_{b}(f(x)) ), donde ( b > 0 ) y ( b neq 1 ).	El argumento (f(x)) debe ser estrictamente positivo ((f(x) > 0)). Se deben encontrar los valores de (x) para los cuales (f(x) > 0).
Funciones Exponenciales	Funciones de la forma ( b^{f(x)} ), donde ( b > 0 ) y ( b neq 1 ).	El dominio es todos los números reales ((mathbb{R})), ya que se pueden evaluar para cualquier valor real de (x).
Funciones Trigonométricas	Funciones como ( sin(x) ), ( cos(x) ), ( tan(x) ), etc.	Para ( sin(x) ) y ( cos(x) ), el dominio es todos los números reales. Para ( tan(x) ), se excluyen los valores donde ( cos(x) = 0 ) (por ejemplo, (x neq frac{pi}{2} + kpi), donde (k) es un entero).
Funciones con Valor Absoluto	Funciones de la forma ( |f(x)| ).	El dominio es todos los números reales ((mathbb{R})), ya que el valor absoluto está definido para cualquier número real.

Si quieres conocer otros artículos parecidos a Cómo calcular el dominio de una función. Ejercicios puedes visitar la categoría Bachillerato.