"La geometría tiene dos grandes tesoros: uno es el teorema de Pitágoras y el otro la razón áurea” J.Kepler
Posiblemente, el teorema de Pitágoras es el resultado matemático más conocido entre los ciudadanos (grandes y pequeños) de todo el mundo. Y sus razones tiene. Sobre todo por sus aplicaciones y su importancia.
Pero, ¿qué sabes de Pitágoras?
Definiciones previas
- Teorema: Básicamente un teorema es un enunciado o proposición cuya verdad es absoluta, y se puede demostrar. Normalmente se parte de una hipótesis o supuesto para llegar a una conclusión o tesis. Aunque se acabe el mundo, un teorema seguirá siendo cierto, es eterno.
- Triángulo rectángulo: Es aquel que tiene un ángulo recto, de 90 grados
- Hipotenusa: Es el lado de mayor longitud de un triángulo rectángulo. Siempre es el lado opuesto al ángulo recto.
- Catetos: Son los dos lados de un triángulo rectángulo que tienen en común al ángulo recto.
Debes saber distinguir muy bien entre el cateto y la hipotenusa.
A algunos alumnos les cuesta identificar la hipotenusa. Para que quede totalmente claro, puedes verlo en las siguientes imágenes:
En cualquier triángulo rectángulo puedes comprobar fácilmente que la longitud de la hipotenusa siempre es mayor que la longitud de los catetos.
¿Qué dice el teorema de Pitágoras?
“En cualquier triángulo rectángulo, el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos”
Es decir, siempre se cumplirá esto:
Por ejemplo si tenemos un triángulo rectángulo cuya hipotenusa mide 5 cm. y sus catetos miden 3 y 4 cm. respectivamente, tendremos que \({ 5 }^{ 2 }={ 3 }^{ 2 }+{ 4 }^{ 2 }\) Es completamente cierto que 25=9+16
No es necesario, ni aconsejable, que te aprendas la fórmula del teorema de Pitágoras. Es mejor que lo comprendas que memorizar que c2=a2+b2 . Porque si te cambian las letras, la lías parda ...
Tres números naturales (los de contar) que cumplen la igualdad que establece el teorema de Pitágoras se llaman ternas pitagóricas. En nuestro caso {3,4,5}
¿Cómo podemos encontrar ternas pitagóricas? De forma muy sencilla. Por ejemplo multiplicando por una constante, por un número positivo. Es decir también son ternas pitagóricas {6,8 y 10}, {9,12 y 15},{4’5,6 y 7’5},… Las hemos conseguido multiplicando por 2,3 y 1’5 respectivamente. Lógicamente hay infinitas.
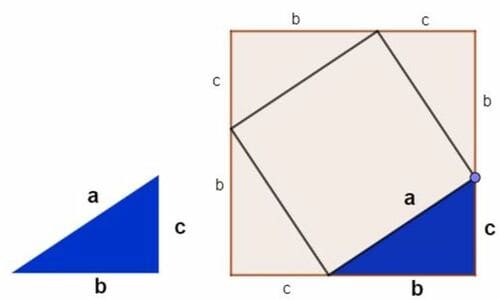
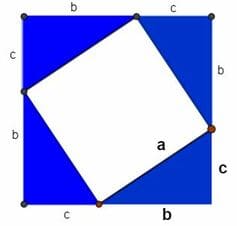
Otra forma de expresar el Teorema de Pitágoras es geométricamente. Viene a decirnos que el área del cuadrado situado sobre el lado de la hipotenusa es exactamente igual a la suma de las áreas de los otros dos cuadrados, que están situados sobre los catetos. En imágenes, algo tan bonito como esto:
La imagen de arriba puedes demostrarla en un periquete, pero para los incrédulos, aquí os dejo una de las mejores demostraciones visuales que existen sobre el teorema de Pitágoras.

Aplicaciones del teorema de Pitágoras
Esta verdad universal nos permite relacionar los tres lados de un triángulo rectángulo. Por tanto es de una utilidad enorme, porque si conocemos dos de ellos, podremos conocer el valor del tercero.
También podemos saber, dados tres lados, si se trata de un triángulo rectángulo. Obviamente, sólo lo será si las longitudes de sus lados cumplen la igualdad del teorema de Pitágoras.
Calcular la hipotenusa conociendo los dos catetos
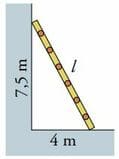
Una escalera cuyo pie está a 4 m de la pared se apoya en esta, alcanzando una altura de 7,5 m. ¿Cuánto mide la escalera? Siempre recomiendo hacer un dibujo para que sea más fácil resolver problemas.
Se observa fácilmente que tenemos un triángulo rectángulo. Por tanto podemos hacer uso del teorema de Pitágoras.
\({ l }^{ 2 }={ 4 }^{ 2 }+{ 7'5 }^{ 2 }\) \({ l }^{ 2 }=16+56.25\)\({ l }^{ 2 }=72'25\) \( l = \sqrt{72.25} = \pm 8.5 \)
Es decir, nuestra escalera mide 8’5 metros. Descartamos el valor negativo, porque no tiene sentido hablar de longitudes negativas.
Ahora ya puedes calcular, por ejemplo, cuánto mide la diagonal de una televisión (un rectángulo que puedo dividir en dos triángulos rectángulos) o saber la máxima distancia que puede recorrer un jugador de fútbol en línea recta. Recuerda que la clave es dibujar triángulos rectángulos. Y no tener dificultades en calcular la raíz cuadrada de un número.
Cómo calcular un cateto conociendo los otros lados
Un poste de 14,5 m de alto se quiebra por su base y cae sobre un edificio que se encuentra a 10 m de él. ¿Cuál es la altura a la que golpea?
Veamos la situación y dibujemos nuestro triángulo con los datos del problema.
En este caso volvemos a plantear la igualdad que establece el teorema pitagórico.
\({ 14'5 }^{ 2 }={ 10 }^{ 2 }+{ x }^{ 2 }\) \(110'25={ x }^{ 2 }\) \( x = \sqrt{110.25} = \pm 10.5 \)
Es decir, los que viven en el tercer piso, a 10’5 metros de altura, lo tienen crudo 😉
Calcular distancias o áreas de cualquier polígono
En muchos casos, podemos encontrarnos con diferentes figuras geométricas, como un triángulo equilátero, donde aplicar la fórmula del teorema. Aunque inicialmente no veas el triángulo rectángulo, lo único que tienes que hacer es buscarlo para poder calcular alguna medida que en principio desconocemos. Veamos algunos ejemplos.
Las diagonales de un rombo miden 10 cm y 24 cm. Hallar su perímetro.
Siempre es importante que hagas un dibujo. Recuerda que el perímetro es la suma de todos los lados.
En este caso, pronto encontramos un triángulo rectángulo, y concluimos que su hipotenusa tiene una longitud de 13 cm. Por tanto, el perímetro será de 4·13=52 cm.
No quiero extenderme aquí, pero debes saber que gracias al teorema de Pitágoras podrás calcular la mayoría de áreas y perímetros de figuras planas. Por ejemplo, ¿eres capaz de calcular la diagonal de este trapecio? Puedes decirme tu solución en los comentarios.
Aprende más sobre ...
Los lados determinan el tipo de triángulo
Equivale a decir que podemos comprobar si tenemos un triángulo rectángulo, conocidos sus tres lados.
Indicar si los siguientes segmentos forman triángulos rectángulos:
- a) 18 cm, 24 cm, 30 cm.
- b) 4 cm, 12 cm, 15 cm.
Veamos el primer caso. Ten en cuenta que la hipotenusa es el lado de mayor longitud. Se debe cumplir que
\({ 30 }^{ 2 }={ 18 }^{ 2 }+{ 24 }^{ 2 }\) \(900=324+576\)
Como la igualdad es cierta, se trata de un triángulo rectángulo.
En el caso b) se observa que \({ 15 }^{ 2 }>{ 4 }^{ 2 }+{ 12 }^{ 2 }\) porque \(225>16+144\)
En este caso estamos ante un triángulo obtusángulo (aquel que tiene un ángulo obtuso, mayor de 90 grados). ¿Cómo lo sé? Porque es una de las consecuencias del teorema de Pitágoras. Me explico:
Llamando c al lado mayor del triángulo, podemos tener tres posibles casos:
\({ c }^{ 2 }={ a }^{ 2 }+{ b }^{ 2 }\) → triángulo rectángulo
\({ c }^{ 2 }>{ a }^{ 2 }+{ b }^{ 2 }\) → triángulo obtusángulo
\({ c }^{ 2 }<{ a }^{ 2 }+{ b }^{ 2 }\) → triángulo acutángulo (sus tres ángulos son agudos, miden menos de 90º)
Con este teorema, también podrás calcular el área y volumen de un prisma, y muchas cosas más.
Demostraciones del teorema de Pitágoras
A lo largo de la fascinante historia de la matemática, se cuentan por cientos las demostraciones de este famoso teorema. Como las que demostraron grandes matemáticos como Platón, Euclides,Pappus o Leonardo da Vinci.
# Demostración 1
Es sencilla, y data del año 1000 a.C., curiosamente cinco siglos antes de que naciera el que algunos consideran el padre de las Matemáticas. Si lo prefieres, puedes verla en un vídeo que hice hace mucho tiempo.

Sea el triángulo rectángulo de hipotenusa a y catetos b,c. Construimos un cuadrado de lado b+c
Usando el mismo cuadrado, vemos que nuestro triángulo rectángulo azul, se puede trazar en las esquinas del cuadrado. Se observa con claridad en la siguiente imagen:
\( \text{Área del cuadrado grande: } (b+c)^2 = b^2 + c^2 + 2bc \quad (1) \)\( \text{Área del cuadrado grande: } a^2 + 4\left(\frac{bc}{2}\right) = a^2 + 2bc \quad (2) \)\( (1) = (2) \quad b^2 + c^2 + 2bc = 2bc + a^2 \quad \rightarrow \quad a^2 = b^2 + c^2 \)
# Demostración 2
Para entenderla, deberás saber conceptos de semejanza de triángulos y sistemas de ecuaciones.
Sea el triángulo ABC recto en A, trazamos la altura (h) correspondiente al lado BC, que corta en el punto D
Definimos los lados a,b,c, siendo a=m+n, donde m=CD y n=DB
Ahora debes estar atento. Observa que los triángulos ABC y ABD son semejantes, al tener un ángulo recto y otro común (el marcado como α). Recuerda que dos triángulos son semejantes si tienen dos ángulos respectivamente iguales, de tal forma que pueden colocarse en posición de Tales. Análogamente ocurre con los triángulos ABC y ADC.
Por semejanza entre \( \triangle ABC \) y \( \triangle ABD \), tenemos que:
\[ \frac{c}{a} = \frac{n}{c} \quad \longrightarrow \quad c^2 = an \quad (3) \]
De forma análoga, mediante semejanza entre \( \triangle ABC \) y \( \triangle ADC \), obtenemos que:
\[ \frac{b}{a} = \frac{m}{b} \quad \longrightarrow \quad b^2 = ma \quad (4) \]
Finalmente, sumando las ecuaciones (3) y (4) obtenemos:
\[ b^2 + c^2 = a(m + n) \quad \longrightarrow \quad b^2 + c^2 = a^2 \quad \text{como queríamos demostrar} \]
Consecuencias del teorema
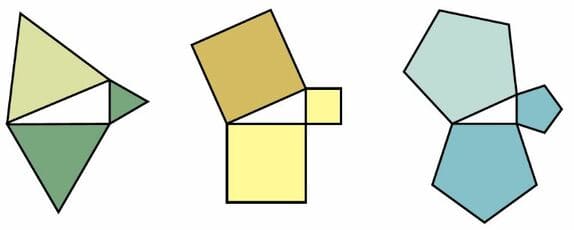
¿Sólo pueden jugar los cuadrados? ¡No! Otros polígonos y figuras curvas también se apuntan a esta fiesta matemática. Veamos brevemente lo que se conoce como el teorema de la semejanza. Aquí tienes la imagen, antes de soltarte el rollete.
Dicho de forma matemática. Si construimos sobre los lados de un triángulo rectángulo como lados homólogos, polígonos semejantes, el área del polígono correspondiente a la hipotenusa, es la suma de las áreas de los polígonos correspondientes a los catetos.
Esto deja evidencias que las matemáticas son principalmente un medio para razonar, no sólo para calcular.
Incluso podríamos hablar de hipopótamos, en una demostración sin palabras …
Podría extenderme mucho más, pero creo que ya es suficiente. Espero que te haya gustado y pueda serte útil.
Posiblemente el teorema de Pitágoras es uno de los más influyentes en la historia de la humanidad, al describir la relación existente entre los lados de un triángulo rectángulo. Estos conceptos han sido fundamentales para conrctar el álgebra y la geometría.
Te agradecería mucho que compartieras este artículo. También puedes dejar tu comentario acerca de este fantástico teorema.
Aprende más sobre ...
¡Felices matemáticas!
Espero que te haya gustado este artículo sobre Teorema de Pitágoras. De 0 a 100. Me ayudarás mucho si lo compartes en tus redes sociales. Debajo tienes los botones🎯¡Hasta pronto!
-
-
Muy agradecido po tus palabras.
Un abrazo
-
-
Muy buen post. Gracias por compartirlo.
-
Muchas gracias Mar. Tengo una hermana que se llama como tú, y también es muy agradecida.
Un abrazo.
-
-
Estimado Justo, hoy que los niños y jóvenes recurren a la web para casi todo lo vinculado a la enseñanza, frente a temas particulares que les toca ver a mis hijas , yo les doy mis libros y ellas prefieren primero ir a la web. En fin son las realidades de hoy. Hoy yo las he imitado, de este tema luego de recorrer a varias web he llegando a esta que me ha impresionado gratamente, muy buena. Mis estímulos y felicitaciones. Continuaré recurriendo a ella.
Eduardo, docente universitario en Ciencias Económicas.-
Leer este tipo de comentarios siempre es muy reconfortante.
Muchas gracias Eduardo. Un abrazo!
-
-
muy buenos días excelente material buen aporte tanto para maestros como para alumnos, tambien se puede demostrar con semicirculos
-
Buenas tardes al otro lado del charco. Muchas gracias por tu comentario Guadalupe.
Un abrazo
-
-
Pues mira por donde, que a mi edad ya longeva, acabo de descubrir que cualquier polígono regular construido sobre los lados de un triángulo rectángulo también cumple el teorema de Pitágoras. Siempre lo había visto solo con cuadrados. Muchas gracias Justo Fernández por tu aportación y claridad en exponerla.
Josep Mauri. (exprofe ya lejano)-
Gracias a tí por tu comentario Josep. La verdad es que yo estoy aprendiendo todos los días algo nuevo.
Espero que hayas disfrutado con tus alumnos tanto como yo. Ahora te toca disfrutar de la vida en tu tercera juventud.
Un abrazo
-
-
Me ha parecido un artículo muy completo.
-
Me alegro que te haya gustado María.
Gracias por comentar. ¡Saludos!
-
-
como decía mi profesor de matemáticas LQQD. demuestra que nuestros conocimientos nunca concluyen, pues si solo me acordaba del nombre "Teorema de Pitágoras" ahora recién comprendo algo más. y gracias. por desasnarme en este siglo del conocimiento.
-
Muchas gracias por tu acertado comentario. Además acabo de aprender una palabra muy poco usada.
Desasnar: educar a una persona para que pierda su rudeza o tosquedad.
Un abrazo!
-
-
En las matemáticas, el contenido o tema de enseñanza debe ir paralelo con su desarrollo histórico, al alumno le gusta y asimila mejor el contenido a tratar. El Teorema de Pitágoras tiene una riqueza histórica excepcional y ningún docente debe perder esa oportunidad. Le envío la terna número 27 que tiene catetos continuos. Donde x^2 + (x + 1)^2 = z^2
(282229692287738524679, 282229692287738524680, 399133058537705128729)
Espero que alguien me envíe la terna número 28.
Muy agradecido y fraternos saludos-
¡Qué respuesta tan interesante y acertada! La verdad es que desconocía la igualdad que muestras. Tendré que investigar.
Muchas gracias por tu comentario José. ¡Saludos!
-
-
Magnífico artículo sobre el teorema de Pitágoras. Se condensa información. Muy instructivo. Enhorabuena al profesor Justo Fernández.
-
Muchas gracias Francisco. Te agradezco muchísimo tus palabras.
¡Un abrazo!-
Saludos y gracias por hacer divertida la matemática
-
Muchas gracias por cargarme las pilas. Un abrazo
-
-
-
-
Excelente recurso para fortalecer la capacidad de razonamiento lógico matemático que mucha falta hace a estudiantes y maestros en sentido general.
Grato con este tipo de publicaciones.
-
Muchas gracias. No te falta razón, buena reflexión.
Un abrazo.
-
-
De nuevo muchas gracias.
-
De nada Manuel. A tí por estar ahí.
Un abrazo! -
Dios habla con las matemáticas y Pitágoras fue su traductor.
-
Interesante refñexión Héctor.
Un abrazo
-
-
-
buen material, apto para los estudiantes que tienen alguna dificultad de aprender, se agradece que lo compartan
-
Gracias Juan. Creo que la mayoría de personas pueden aprender algo en esta entrada.
Saludos.
-
-
Es genial lo que estás haciendo, muchas gracias
-
¡Muchas gracias Juan Carlos!
Todos vuestros mensajes de ánimo me hacen continuar con más fuerza divulgando las matemáticas.
Un abrazo!
-
-
MIL GRACIAS POR COMPARTIR LA INFORMACIÓN DE UNA FORMA MUY PRECISA, DIDÁCTICA E INTERESANTE!
-
I love you Ana!
Gracias por tu agradable comentario. ¡Un abrazo!
-
-
Se agradece todo el material
-
Selma, yo agradezco mucho tener tan buenos lectores como tú.
Un abrazo!
-
-
Excelente material para explicar el teorema de pitagoras, muchas gracias por tu aportación que sirve para que los alumnos lo entiendan de una manera muy sencilla.
-
Esa siempre ha sido mi intención, buscar la forma más sencilla de explicar las mates a los alumnos.
Gracias Annel. ¡Saludos!
-
-
Si! Efectivamente es un regalo para mi y para mis alumnos...este es uno de los mas hermosos temas que tiene la Matemática, es como un "hito" en el pensamiento del estudiante, una vez que logra aprenderlo. Me alegro y te felicito: hermosa redacción. Gracias
-
Muchas gracias Fanny! Estroy de acuerdo contigo. Es cierto que algo en la mente del estudiante hace clic cuando por vez primera atisba y descubre la belleza y el enorme potencial de las matemáticas.
Un abrazo!
-
-
Un saludo desde Chile, tierra de poetas como Gabriela Mistral y Pablo Neruda, de grandes hombres como Salvador Allende y también de seres abyectos como (no quiero nombrarlo). Soy un aficionado a las matemáticas y la lógica enamorado de hypatia, disfruto con los temas y como los tratas. Gracias
-
Gracias por tu comentario Eduardo. ¡Viva Chile!
-
-
Muy interesante el artículo, porque realza aspectos históricos relacionado con el teorema...
-
Creo que siempre es importante introducir el contexto histórico en la enseñanza de las matemáticas.
Gracias Hugo! Saludos!
-
-
Excelente artículo, claro y detallado.
Agradecido por tu referencia a mi blog sobre la demostración de Leonardo-
Gracias! Me gustó mucho la demostración del genio Da Vinci que aparece en tu blog. Invito a los lectores a que la conozcan aquí
-
-
Hola, excelente material, la explicación es sencilla, clara y con buenos ejemplos y demostraciones. ¡Gracias!
-
Me alegro que te haya gustado Rubén. Gracias a tí por comentar.
¡Saludos! -
Claro y conciso. Excelente material. Muchísimas gracias. Saludos.
-
Muy agradecido por tus palabras. Un abrazo Liliana
-
-
-
Ojalá fuese profesora de Matemáticas para usar tus excelentes materiales en las clases. Un gran trabajo. Muchas gracias por compartirlo!!
-
Wow, que palabras más bonitas Aleida. Me has sacado una gran sonrisa.
Muchas gracias. ¡Un abrazo!
-
-
Me ha encantado. Soy matemática y me ha sorprendido en muchas cosas y aplicaciones, me encanta la geometría.
-
¡Gracias Maite! Me alegro que te haya sorprendido. A mí también me encanta la geometría. Junto con el álgebra, creo que es mi rama favorita de las mates.
Un abrazo. -
Excelente material para ponerlo en práctica con mis estudiantes de matemáticas está haciendo un gran aporte a la educación tanto a los docentes como a los estudiantes me gustaría si es posible me siguiera enviando material de matemáticas para secundaria de sexto a once. Gracias por su labor
-
Me alegra saber que te gustan los artículos que publico.Gracias.
Siempre que pueda iré añadiendo entradas al blog.
Un saludo Wilson.
-
-
-
Muy buena contribución. Incluyendo las demostraciones.
Usaré este post en clase sin duda alguna.
Enhorabuena por la exposición.-
Muchísimas gracias Gonzalo. Cuánto me alegra leer estos comentarios.
¡Un abrazo!-
Buenos días desde Chile.
Excelente material, será de gran utilidad para mis alumnos cuando tenga que enseñar este contenido.
Se lo daré como referencia.
Saludos.-
Muchas gracias Alexis. Que bien poder ayudar. ¡Saludos para Chile!
-
-
-
58 lectores opinan:
Deja una respuesta










Gracias por hacer de las matemáticas algo entretenido, novedoso y a la vez educativo.