
Azar y probabilidad son conceptos un poco resbaladizos para mucha gente. ¿Me puede tocar a mí? ¿Es probable? ¿Es cierta la ley de Murphy? ¿Es posible que llueva mañana?
Probablemente estas preguntas son bastante frecuentes. Es por esto que la probabilidad de sucesos es una rama de las matemáticas con muchas aplicaciones.
— ¡Por fin las matemáticas valen para algo! (je,eje)
Cierto, habitualmente los alumnos suelen ver más atractiva una clase donde puedan aplicar lo aprendido en su vida cotidiana. Aquí no tienen escusas. Cada vez nos parecemos más a los ingleses, y apostamos por muchas cosas, sobre todo cuando hay experimentos aleatorios de por medio.
Azar y probabilidad
El azar y la probabilidad son conceptos estrechamente relacionados en el ámbito de las matemáticas y la estadística. El azar se refiere a la ocurrencia de eventos o sucesos de manera impredecible, sin una causa aparente o conocida. Por otro lado, la probabilidad se encarga de medir y cuantificar las posibilidades de que ocurra un determinado evento. Ambos conceptos son fundamentales para comprender el mundo que nos rodea y tomar decisiones informadas.
La probabilidad se expresa como un número entre 0 y 1, donde 0 representa la certeza de que un evento no ocurrirá, y 1 representa la certeza de que un evento sí ocurrirá. Por ejemplo, si lanzamos una moneda al aire, la probabilidad de que caiga cara es de 0.5, ya que existen dos posibles resultados igualmente probables: cara o cruz. La probabilidad se calcula dividiendo el número de casos favorables entre el número total de casos posibles.
El azar, por su parte, es una característica inherente a muchos aspectos de nuestra vida cotidiana. Desde el lanzamiento de un dado hasta el resultado de una lotería, el azar está presente en numerosas situaciones. Sin embargo, a pesar de su aparente impredecibilidad, el azar sigue ciertas regularidades estadísticas. A través de la teoría de la probabilidad, podemos entender y predecir patrones en eventos aleatorios, lo que nos permite tomar decisiones más informadas y minimizar los riesgos.
La probabilidad y el azar son herramientas fundamentales en campos como la estadística, la economía, la física y la biología, entre otros. Nos permiten analizar y comprender fenómenos complejos, modelar situaciones de incertidumbre y tomar decisiones basadas en datos. Además, el estudio de la probabilidad nos ayuda a entender mejor cómo se comportan los sistemas y cómo se distribuyen los sucesos en el mundo que nos rodea.
Probabilidades de sucesos
Probabilidad y posibilidad son palabras que usamos casi todos los días para intentar responder a las muchas preguntas.
La famosa teoría de la probabilidad es importante. Pero yo me pregunto: ¿cómo demonios se puede cuantificar una teoría en la cual interviene la incertidumbre? ¿no son las matemáticas una ciencia exacta?
¿Somos capaces de pronosticar el futuro con absoluta certeza? ¡Claro que no! Por esta razón, la necesidad de esquivar la incertidumbre nos lleva a utilizar la teoría de la probabilidad de sucesos.
Juegos de azar. El origen del cálculo de probabilidades
Los juegos de azar han acompañado a la humanidad desde sus orígenes. Se han encontrado pinturas sobre juegos de azar en las pirámides de Egipto. En la antigua Grecia y en Roma, utilizaban la combinación resultante de tirar cuatro dados para predecir el futuro y revelar la voluntad de los dioses ...
Resulta bastante sorprendente que los griegos, grandes precursores de las matemáticas, no percibieran la importancia de la simetría de los dados para desarrollar una teoría de la probabilidad.
Pero no es hasta bien entrado el siglo XVII cuando esta rama de las matemáticas empieza a asentar sus bases, mostrando un cierto formalismo con Fermat y Pascal. Y más tarde con De Moivre, Laplace y Gauss.
¿Sabes que puedes calcular probabilidades con el triángulo de Pascal? Creo que al artículo te resultará interesante
Hoy día, en la maravillosa época que nos ha tocado vivir, la teoría de la probabilidad se aplica en muchísimos campos. Es difícil encontrar alguna disciplina donde no se utilice. El primero en formular una definición de probabilidad de sucesos fue Jakob Bernoulli (un integrante de la familia más científica de todos los tiempos). En su obra "El Arte de Predecir" (1713), ya incluye proporciones de posibilidades respecto del total. Era un concepto de frecuencias, repitiendo un proceso muchas veces.
En numerosas ocasiones necesitamos evaluar cuidadosamente la incertidumbre utilizando matemáticas, en este caso aplicando probabilidad y estadística.
Tipos de probabilidad
— ¿Tipos? Qué corcho! , sólo hay una, mi mala suerte!
— No, no me refiero a la suerte. Esa hay que buscarla.
Te cuento, hay tres tipos de probabilidad:
# Probabilidad geométrica
Es la que está basada en las simetrías. ¿Cuál es la probabilidad de sacar un 7 al tirar dos dados?
Cómo existen 6 formas distintas de obtener un siete, sobre un total de 36 posibilidades, decimos que la probabilidad es 1/6.
# Probabilidad empírica
En segundo lugar te puedes encontrar con la probabilidad "empírica", como la que tiene una persona de vivir más de 80 años, que se basa en las estadísticas recogidas en el pasado. (seguro que muchas veces recurres a ella sin darte cuenta)
# Juicios de probabilidad
Finalmente existen los "juicios de probabilidad", como las probabilidades que existen de que tu equipo gane el partido. (aquí toma protagonismo tu intuición y tu conocimiento) Aunque sean a menudo distintos, los tres conceptos se utilizan a veces sin ningún tipo de distinción. Incluso en programas de televisión, suelen llegar a conclusiones erróneas. A menudo, cuando los argumentos estadísticos (y la política) se ven enmarañados por la casualidad, los errores aparecen por todas partes ...
Aprende más sobre ...
Anécdotas históricas relacionadas con la probabilidad
A Chevalier de Meré le gustaba frecuentar los salones de juego de la época. En la Francia del siglo XVII eran muy aficionados a los juegos de azar y a llevar tremendos pelucones. Tuvo bastantes conversaciones con Pascal y con Fermat porque estaba interesado en el juego de tirar tres dados y sumar los puntos que resultaban.
El que apostaba a un número y ganaba, se llevaba la pasta. Era el inicio de los casinos ... Y ellos jugaban con ventaja. Dedujeron que los resultados 10 y 11 eran los más probables. ¿Por qué? Cuestión de probabilidades. Si sigues leyendo lo entenderás.
¿Hicieron mucho dinero estos ilustres matemáticos? Parece ser que sí ...
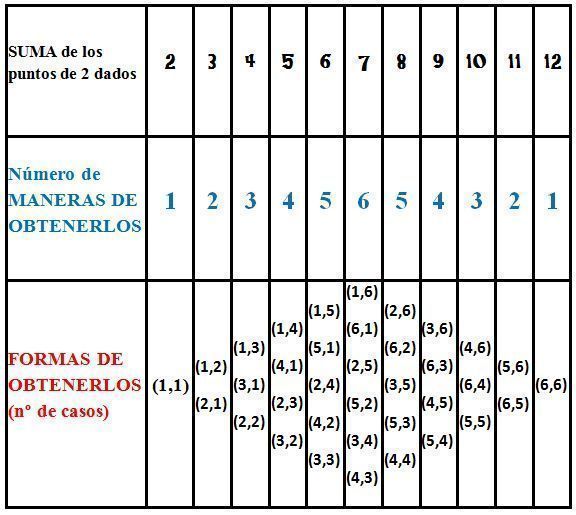
Para que puedas entenderlo, te explicaré un ejemplo con dos dados ¿Cuál es el resultado más probable si sumamos los puntos de los dos dados? En este caso es más sencillo. Lo más probable es obtener 7, porque hay 6 formas diferentes de obtener estos punto, frente a los 36 casos posibles. Con la siguiente imagen lo verás mejor.
Siempre es necesario disponer del espacio muestral, para poder calcular la probabilidad de que salga lo que nos interese. Y saber los casos favorables y los casos posibles.
También es conocida otra preguntilla que se sacó debajo de su peluca: "¿Qué es más probable, sacar un 6 en cuatro tiradas de un dado, o sacar un "seis doble" en 34 tiradas con dos dados? ¿A qué opción apostarías? Si te atreves, puedes dejar tu opinión en los comentarios.
D'Alembert, otro genio matemático que intervino en la ilustración francesa del siglo XVIII, quiso comprobar la probabilidad de obtener cara y cruz al lanzar dos monedas. Puedes ponerte en situación y realizar el experimento ...
En principio, ¿qué probabilidad piensas que obtendrías?
Puedes seguirme en Twitter para poder ver este tipo de encuestas. Suelen ser interesante conocer los resultados:
¿Cuál es la probabilidad de obtener cara y cruz al lanzar dos monedas?
— soymatematicas.com (@soymatematicas) February 15, 2016
D'Alambert concluyó que la probabilidad era 1/3. ¡Se equivocó! Al igual que bastantes de los que participaron en la encuesta (algunos con ayuda de Google 😉
En la siguiente imagen tienes un ejemplo de azar y probabilidad. Aquí podrás comprobar y entender que la probabilidad es 1/2.
Una equivocación de un ilustre matemático. Sí, los genios también se equivocan ... En cierto modo es comprensible, porque todavía no tenía los conceptos bien asentados.
Esto es un simple ejemplo para que veas que los problemas de probabilidades de sucesos tienen una cierta dificultad. Es muy importante que te acostumbres a decidir y cuantificar problemas cotidianos a números, para poder hacer los cálculos. Esto no siempre resulta fácil. Practicando y haciendo ejercicios todo se aprende.
Azar y probabilidad son onsiderados cómo algo opuesto al orden, pero has podido ver que también el azar tiene sus regularidades. ¡Podemos descubrir sus leyes! Y así, en cierta medida, gobernarlo.
En resumen, el azar y la probabilidad son conceptos estrechamente relacionados que nos permiten comprender y predecir eventos aleatorios. A través de la probabilidad, podemos cuantificar las posibilidades de que ocurra un evento específico, mientras que el azar nos muestra la impredecibilidad inherente a muchos aspectos de nuestra vida. Estos conceptos son esenciales en numerosas disciplinas y nos ayudan a tomar decisiones informadas y comprender mejor el mundo que nos rodea.
Azar y probabilidad en matemáticas
En el fascinante mundo de las matemáticas, el azar y la probabilidad juegan un papel fundamental. El azar, ese elemento impredecible e incierto, se encuentra presente en gran cantidad de situaciones de nuestra vida cotidiana. Sin embargo, a pesar de su aparente caos, es posible encontrar regularidades y patrones que nos permiten calcular y predecir los resultados de diferentes eventos.
La probabilidad es la rama de las matemáticas encargada de estudiar los sucesos aleatorios y determinar la posibilidad de que ocurran. Se basa en el análisis de los diferentes resultados posibles y la asignación de valores numéricos a cada uno de ellos. Estos valores, llamados probabilidades, representan la medida de certeza o incertidumbre de que un determinado evento se produzca.
Para comprender mejor la probabilidad, es importante entender algunos conceptos fundamentales. Uno de ellos es el espacio muestral, que representa el conjunto de todos los posibles resultados de un experimento aleatorio. Por ejemplo, si lanzamos un dado, el espacio muestral sería {1, 2, 3, 4, 5, 6}, ya que esos son todos los números que pueden aparecer al caer el dado.
Otro concepto relevante es el de evento, que es cualquier subconjunto del espacio muestral. Por ejemplo, si queremos determinar la probabilidad de obtener un número par al lanzar un dado, el evento sería {2, 4, 6}. La probabilidad de un evento se calcula dividiendo el número de resultados favorables entre el número total de resultados posibles.
Aprende más sobre ...
El cálculo de probabilidades nos permite tomar decisiones informadas y predecir el comportamiento de sucesos aleatorios. Además, la probabilidad se aplica en diversas áreas, como la estadística, la teoría de juegos, la economía y la física, entre otras. Su estudio nos ayuda a entender mejor el mundo que nos rodea y nos brinda herramientas para tomar decisiones racionales en situaciones de incertidumbre. Si te has quedado con ganas de aprender más, aquí tienes un formulario de probabilidad.
Espero que te haya gustado este artículo sobre Azar y probabilidad de sucesos. Las regularidades del azar. Me ayudarás mucho si lo compartes en tus redes sociales. Debajo tienes los botones🎯¡Hasta pronto!
-
Tiene muchas palabras que probablemente podrían confundir a las personas que leen esto, la información esta muy bien, y es explicada de una manera muy buena
-
Hola Justo, gracias por tu fantástica web, el caso es que estoy trabajando con una web de lotería y como sabrás, ha habido cambios en Euromillones, han añadido una estrella más, en Internet he encontrado una tabla de probabilidades para una apuesta simple que comparten muchas webs y, dado que desde EGB soy un poco "bruto" no se si es correcta, la verdad, me extraña que haya un salto tan grande de probabilidad de la primera categoría a la segunda (suponiendo que sean correctas), te pego la tabla
Categoría premio Probabilidad
1ª (5+2) 1 entre 139.838.160
2ª (5+1) 1 entre 6.991.908¿sería mucho pedir que me confirmaras si es correcto o no? no se a quién pedírselo...
Gracias!
-
me gustaría saber que es una función
-
Yarina una función es una relación entre dos variables (magnitudes que varían) a las que, en general, llamamos x e y.
La expresión "es una función de ..." significa "depende de ..."
Por ejemplo, la temperatura del aire es función de la altura (depende de la altura).Saludos!
-
-
Gracias Justo, creo lo mismo que es bien complicado. Saludos y éxitos!
-
Hola Justo
Mira es muy bueno lo que haces con el tema de las matemáticas. Yo solo soy fan de esas curiosidades y no soy muy conocedor del tema, pero siempre me estoy cuestionando cosas que en un principio a mí me parecen solucionables con la matemática.
Respecto a las probabilidades hace unos meses se me ocurrió un tema y te lo paso a ver qué crees tú.
La cosa es así: en una gran ciudad, digamos de al menos 1 millón de habitantes me paro en una esquina y qué probabilidades tendría de que dos personas que cruzan la calle, sin haberse visto una a la otra, bostecen al mismo tiempo o al menos con menos de un minuto de diferencia?
Mi interés es, en parte, demostrar aquello que reza que el bostezo es contagioso.
Tengo una teoría, pero no me alcanza el conocimiento matemático o probabilístico para calcularlo.
Esto no es respuesta: yo creo que según los horarios de sueño y de comidas de cada cual durante los cuales se suele bostezar más ( que en una ciudad son muy comunes) hay más probabilidad de que eso suceda y no de que sea contagioso.
Tú que crees?
Gracias por cualquier aporte que puedas hacer!!
Saludos
Michel-
Muchas gracias por tu aportación y tus ánimos Michel.
La pregunta que haces es interesante, pero creo que difícil de responder. Supongo que a primeras horas del día, la probabilidad sería mayor . Se podría hacer un estudio estadístico que se pudiera extrapolar, pero es complicado.
Hay bastantes teorías al respecto del bostezo, pero yo también creo que es contagioso. Es más, si alguien ahora lee la palabra BOSTEZO, es posible que bostece, y se quede a gusto en sus trece. ?
Un abrazo Michel
-
7 lectores opinan:
Deja una respuesta






Quiero aprender más sobre: